
Sign chart calculus free#
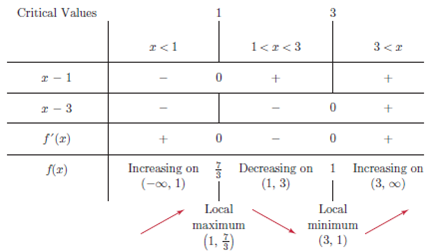
In less than a minute you’ll get your chart instantly You’ll then receive an email with a Free Ebook, Type Report and additional resources NOTE: If you don’t know what your birth time is, Click Here. To get the critical values, we equate the numerator and the. Your chart will identify your Quantum Human Design Type, Authority, Profile, Channels and more with the Traditional HD language in parentheses. Those that satisfy the inequality are included in its solution set. For example, if the derivative of a function f is positive in a certain set of domain values, the students would want to conclude that for that set of domain values, the function f is increasing. In solving rational inequalities, first we get its critical values, then use the values to determine the intervals, and finally, test the values in each interval to see if they satisfy the inequality or not. Once students have made a sign chart they should then explain how the information shown in the sign chart leads to various conclusions. Then using the sign charts students are asked to explain, and support their reasoning, the location of all points of inflection. Students are asked to create a sign chart of f”. Part III: In this part the graph represents a function f(x), the 2nd derivative of f(x). Then using the sign charts students are asked to explain, and support their reasoning, for the location of all relative minima and relative maxima, and all points of inflection. Students are asked to create a sign chart of f’ and f”. Critical points are the points on the graph where the. Part II: In this part the graph represents a function f’(x), the derivative ofį(x). A critical point of a continuous function f f f is a point at which the derivative is zero or undefined. When I talk about the limit of a function f(x). Then using the sign charts students are asked to explain, and support their reasoning, for the location of all relative minima and relative maxima, and all points of inflection. Calculus involves a major shift in perspective and one of the first shifts happens as you start learning limits. Part I: In this part the graph represents a function f(x). This activity is divided into three parts. Points on the graph of a function where the derivative is zero or the derivative does not exist are important to consider in many application problems of. Sign chart calculus calculator Buy tickets & passes online for upcoming events in, live concerts, and events happening in. This product will help students learn how sign charts can be helpful to them. Read the statements on the front cover of Section I and look up when you have finished. For 2nd Derivative Test, suppose f'' is continuous near 0, then if f'(0)=o and f''(o)>0, then f has local min at 0 if f'(o)=0 and f''(0)0, f is increasing on the corresponding range when f'(0)0, f is concave upwards when f''<0, f is concave downwards.Sign charts have been used by students in pre-calculus and calculus to help them summarize the behavior of a function. For 1st Derivative Test, if f' changes from positive to negative at 0, then f has a local max at 0 if f' changes from negative to positive at 0, then f has a local min at 0 if f' does not change signs, 0 is then not local max or min, so you would like to check the two end points for max or min. But that is just possible, so in order to confirm, we need to use 1st Derivative Test or 2nd Derivative Test. Not hard to discover, when f(0)= 0, that is the root of the function: when f'(0)=0, then 0 is a critical number and is possible to be max or min. These have nothing to do with calculus but it is good to know. And if f is just greater than 0 at certain range, then it is just above x-axis at that corresponding range, vise versa. We call this function the derivative of f ( x) and denote it by f ´ ( x ). This slope depends on the value of x that we choose, and so is itself a function. To our common sense, when f is always greater than o, then the function is always above x-axis, and when f is always less than 0, f is always below the x-axis. The Sign of the Derivative Recall from the previous page: Let f ( x) be a function and assume that for each value of x, we can calculate the slope of the tangent to the graph y f ( x ) at x. For other less familiar families of functions, we can use calculus to. possible maximum/minimum (To confirm, use 1st Derivative Test or 2nd Derivative Test) How can we construct first and second derivative sign charts of functions that. root of f (where the function itself crosses the x-axis) Here is a brief summary of this relationship: But for graphing the most important part is to understand the relationship betwwen f, f' and f''.

apply the calculus ideas that we have been studying up to this point in Chapter3. The first derivative of a function is an expression which tells us the slope of a tangent line to the curve at any instant. One of the most important part of calculus is graphing. Construct a first derivative sign chart for f f and thus determine all.


 0 kommentar(er)
0 kommentar(er)
